Rozwijanie logicznego myślenia i wyrównywanie deficytów w tym zakresie, to jedno z podstawowych zadań każdego pedagoga, w szczególności, pedagoga specjalnego. Nasi uczniowie (Zespół Szkół Specjalnych) mają duże kłopoty w zakresie rozwiązywania gier logicznych, rozwiązywania problemów i rozwiązywania zagadek. Stąd wiele naszych działań odnosi się do uzupełniania tych deficytów i niwelowania dysfunkcji, które utrudniają opanowanie technik szkolnych.
Jak to robić, by ćwiczenia i zabawy były na tyle atrakcyjne, by uczniowie chcieli aktywnie i efektywnie w nich uczestniczyć?
Starym naszym zwyczajem proponujemy zabawy z wykorzystaniem kolorowych gadżetów i przedmiotów codziennego użytku, takich jak na przykład kolorowa wycieraczka w grochy, zakupiona w sieci sklepów meblowych IKEA. Koszt takiego gadżetu jest niewielki, bo niespełna 10 zł, a możliwość zabaw nieograniczona.
Proponujemy Państwu kilka logicznych ćwiczeń i zabaw, przy okazji rozwijających techniki szkolne, umiejętności matematyczne, czy gramatyczne. Do zabaw dodatkowo udostępniamy karty pracy i mini plansze z kolorowymi grochami, którą można zalaminować i zanim Państwo zakupicie oryginalną "matę" posłuży do zabaw.
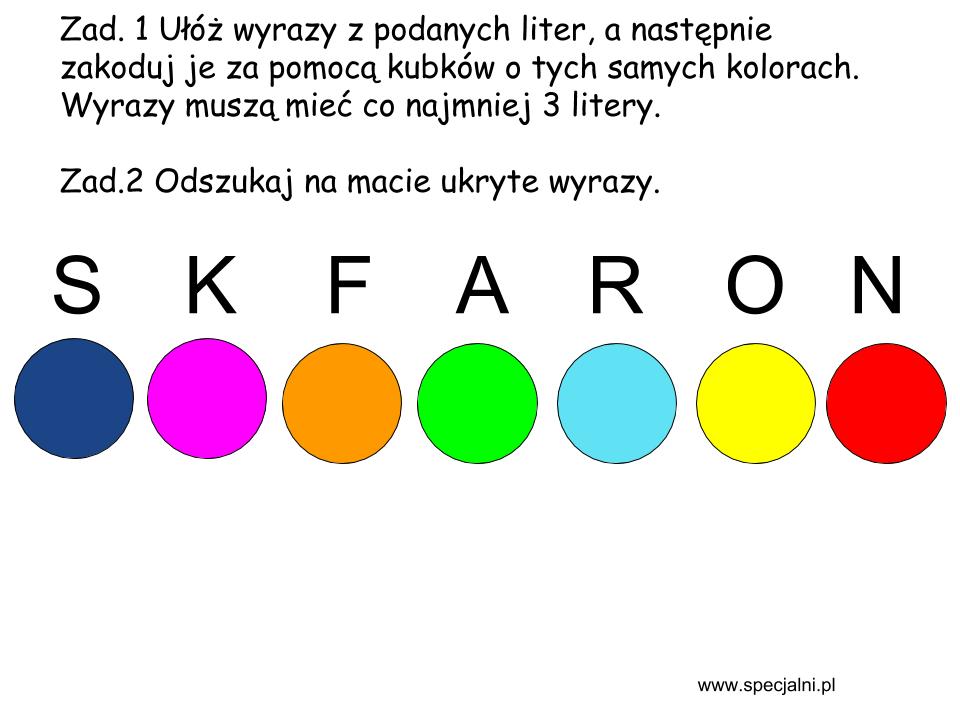
Zad. 1 Polega ono na ułożeniu przez dzieci wyrazów z podanych liter, a następnie zakodowaniu ich za pomocą kubków o tych samych kolorach. Wyrazy muszą mieć co najmniej 3 litery.
Zad.2 Dzieci muszą odszukać na macie ukryte wyrazy pod kolorowymi grochami. Najpierw wyrazy powinny być ułożone w rzędach lub kolumnach, a następnie dzieci mogą odczytywać wyrazy i je układać również po skosie lub przeskakując w dowolny sposób na macie.

Zad. 3 Z kubeczków ułóż liczby dwucyfrowe, trzycyfrowe i większe posługując się zakodowanymi liczbami. Ułóż liczby z kubeczków i odkoduj je. Odczytaj liczby zakodowane na macie. Najpierw poziomo, a następnie pionowo. Zacznij od liczb jednocyfrowych, dwucyfrowych itd. zwiększając stopień trudności. Ułóż na macie kolorowe kubki, a następnie poproś kolegę o odczytanie zakodowanej liczby.
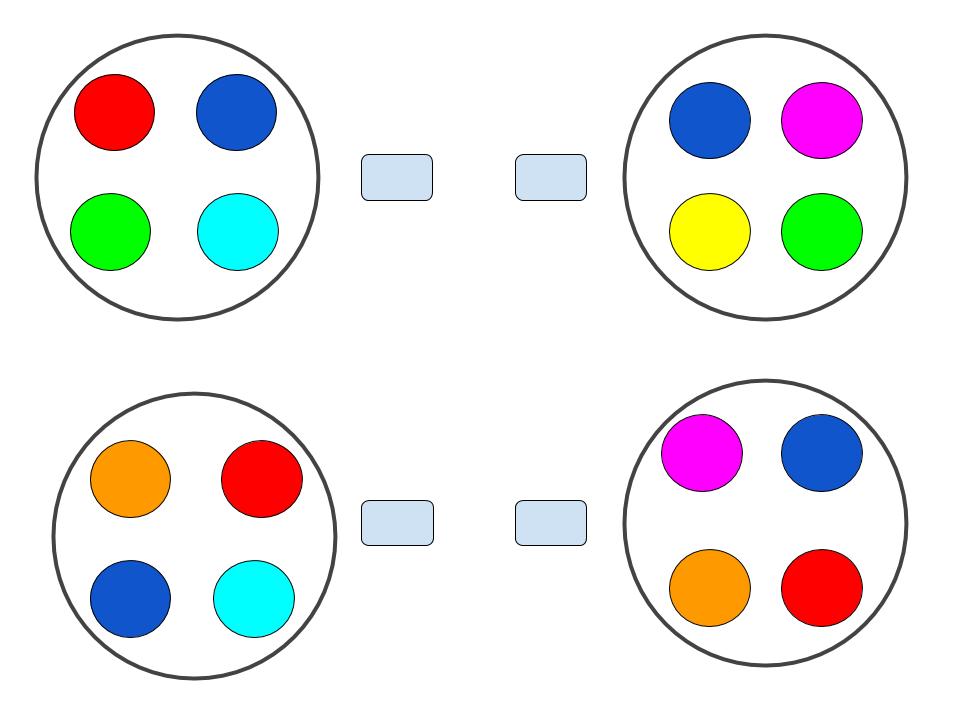
Zad. 4 Doskonalenie działań matematycznych, a przede wszystkim dodawania i odejmowania liczb. Dzieci układają wybrane 3,4,5 czy więcej kubków na odpowiadających im kolorem kółkach. Następnie ich zadaniem jest wskazanie jaka jest ich suma. Takich kombinacji może być wiele.
Dzieci mogą wskazać sumy wszystkich poziomych rzędów, a następnie porównać je. Który rząd ma największą wartość, który najmniejszą i porównywać sumy między różnymi rządami, analogicznie między kolumnami. Inne zadanie może polegać na wskazaniu sumy powstałej w wyniku dodania wszystkich zielonych kółek, lub kółek czerwonych. Następnie możemy poprosić, by wskazać różnicę między danymi kolorami.


Zad. 5 Mata może posłużyć nam do korygowania wad wymowy. Ćwiczenie może polegać na nazywaniu kolorów zamieszczonych na macie, a następnie odczytywaniu ich według różnych kodów. Np, najpierw w rzędach, póżniej w kolumnach. Co drugie kółko, co trzecie itd. Za pomocą kolorów możemy zakodować głoski lub sylaby.
Zad. 6 Kolejne ćwiczenie może polegać na wskazaniu współrzednych konkretnych kolorów i ich zapisania na karcie pracy.


Zad. 7 Zadanie polega na ułożeniu kółka z 4 małymi kropkami w takim miejscu( po środku 4 kółek), aby kolory po każdej z 4 stron odpowiadały tym na macie. Następnie zadaniem ucznia jest dodanie wartości tych kółek i zapisanie na karcie jaka to suma. Wartości danego koloru zamieszczone są na karcie kontrolnej nr 1. (Kółka należy wydrukować, wyciąć i najlepiej zalaminować, bu się nie zniszczyły).

Notka o autorkach: Zyta Czechowska i Jolanta Majkowska- nauczycielki w Zespole Szkół Specjalnych w Kowanówku. Członkinie grupy SuperbelfrzyMini i SuperbelfrzyRP. Autorki bloga specjalni.pl. Entuzjastki nowoczesnych technologii i kreatywnych pomocy dydaktycznych. Wdrażają elementy programowania w szkolnictwie specjalnym. Autorki projektu sieci współpracy nauczycieli, prowadzące Rady Szkoleniowe i warsztaty dla nauczycieli. Za szczególne osiągnięcia edukacyjno-wychowawcze otrzymały w 2017 r. Nagrodę Ministra Edukacji Narodowej. Niniejszy artykuł ukazał się w blogu Zamiast Kserówki. Licencja CC-BY-SA.



















